CHINE (L’Empire du Milieu) - Sciences et techniques en Chine

CHINE (L’Empire du Milieu) - Sciences et techniques en Chine

Pour la Chine, comme pour d’autres civilisations, plus on remonte le temps, plus il devient difficile de préciser ce qu’on doit entendre exactement par «science». C’est pourquoi la «science chinoise» peut se définir de plusieurs manières: il peut s’agir de toute idée, découverte ou méthode chinoise qui joue encore un rôle dans la science actuelle, mais ce peut être aussi l’ensemble des traditions visant à interpréter ou à agir sur la nature qui se sont développées dans le monde chinois. La première définition conduit souvent à présenter le savoir ancien comme un océan d’erreurs duquel émergent de temps à autre les brillantes anticipations de précurseurs géniaux: Zhang Heng (78-139), inventeur du premier sismographe connu, devient géophysicien, l’alchimiste Sun Simo (VII^e s.), biochimiste et, à l’extrême, Zhuangzi, penseur de la relativité. Il en découle donc une classification des savoirs anciens calquée sur les catégories de la science actuelle, supposées a priori universelles et atemporelles. Une telle approche trahit souvent les réalités historiques: parler sans réserves de physique ou de biologie chinoises oblige à regrouper artificiellement des ensembles de faits initialement épars et sans cohérence globale, et contraint à attribuer aux anciens des motivations qui ne pouvaient pas être les leurs. La seconde définition, plus soucieuse d’histoire que de téléologie, vise à comprendre le passé à partir du passé plutôt qu’à partir du présent, et invite à rendre compte d’interactions complexes entre facteurs multiples, internes comme externes, qui ont agi sur la vie des idées dans leur contexte historique: d’où, par exemple, l’éclairage de l’histoire de l’alchimie par le taoïsme, et celui de l’astronomie par le ritualisme divinatoire. Toutefois, il ne faudrait pas confondre sciences, techniques et philosophie, ni oublier qu’il existe des sciences chinoises indépendantes de pratiques magico-religieuses: aucun lien de continuité ne permet d’associer les conceptions protocolaires et emblématiques des nombres propres aux devins de l’Antiquité, dont parle Marcel Granet, à celles purement rationnelles de mathématiciens comme Liu Hui (III^e s.), Zu Chongzhi (V^e s.), Li Shunfeng (VII^e s.).

Plusieurs jugements contradictoires, trop souvent entachés de partialité, ont été portés sur les sciences chinoises. Certains savants, comme le père Gaubil au XVIII^e siècle, ou Jean-Baptiste Biot au XIX^e siècle, ont défendu l’idée d’une très haute antiquité de celles-ci (XXV^e s. av. notre ère). Mais ces déductions reposaient sur des textes apocryphes et sur une chronologie chinoise parfaitement mythique. Pour d’autres, la science chinoise ne serait qu’un ensemble inorganisé de connaissances empiriques, et le peu de vérité qu’on y trouverait ne pourrait s’expliquer que par des emprunts aux autres civilisations: en 1760, Joseph de Guignes écrit un mémoire pour prouver que «les Chinois sont une colonie égyptienne»; au début du XX^e siècle, l’historien japonais Iijima Tadao tente sans grand succès de faire dériver toute l’astronomie chinoise de celle des Babyloniens. En même temps que l’on se sert des ressemblances entre cultures pour conclure à des influences unilatérales de l’Occident sur la Chine, les différences sont jugées révélatrices d’une infériorité chinoise de principe, en vertu du préjugé courant selon lequel tout savoir scientifique ne peut venir que du monde européen, inventeur de la méthode expérimentale et porteur de l’héritage grec. Mais l’idée d’une Europe fermée aux influences extérieures ne se justifie pas davantage que celle d’une Chine ouverte, mais elle-même dépourvue de rayonnement.

En contact avec les civilisations iranienne, hellénistique et romaine dans l’Antiquité, la Chine est en relation avec l’ensemble du continent asiatique sous les Tang. Sous les Mongols, à l’époque des grands voyageurs, les influences réciproques de l’Iran islamisé et de la Chine se font particulièrement sentir: trigonométrie sphérique et instruments astronomiques de Guo Shoujing, d’origine islamique (vers 1279), mais aussi traductions persanes d’ouvrages chinois de médecine, enfin, contacts scientifiques avec l’Europe par l’intermédiaire des missions jésuites à partir de la fin du XVI^e siècle. Pourtant, malgré l’importance de ces échanges, on doit reconnaître que les sciences chinoises forment un ensemble de traditions très différentes de celles de l’Europe, de l’Islam, ou même de l’Inde, car dominées par une perspective «organiciste» (prédominance de la croyance à un ordre général et spontané dans un univers à l’image d’une totalité organique, et dans lequel chaque phénomène se trouve en correspondance continue avec tous les autres, tout en passant par des phases de croissance, maturité et déclin). D’où l’intérêt des penseurs chinois pour les phénomènes impliquant une action à distance (magnétisme, marées, phénomènes sismiques, autorégulation des organismes...) de préférence à ceux qui reposent sur des actions directes et mécaniques; pour l’algèbre plutôt que pour la géométrie et, enfin, pour les théories ondulatoires plutôt que pour les théories atomistiques.

Mathématiques

Les inscriptions sur os et écailles (jiaguwen ) découvertes dans la région de Anyang, dans l’actuelle province du Henan, à la fin du siècle dernier, nous apprennent que, dès les XIV^e-XI^e siècles avant notre ère, les Chinois utilisaient une numération décimale de type «hybride», combinant dix signes fixes pour les unités de 1 à 9, avec des marqueurs de position particuliers pour les dizaines, centaines, milliers et myriades. Aux abords de l’ère chrétienne, le système se stabilise et note déjà les nombres pratiquement de la même manière qu’en chinois moderne. Le zéro-cercle, très probablement d’origine indienne, n’est attesté qu’au XIII^e siècle, mais, auparavant, on ménageait un espace vide pour indiquer les unités manquantes.

Habiles calculateurs, rompus aux opérations sur les grands nombres comme sur les fractions dès le début de notre ère, les Chinois n’ont jamais conçu la mathématique comme une science déductive, mais plutôt comme une logistique reposant sur la manipulation d’instruments, essentiellement le boulier (suanpan ) et les baguettes à calculer (chousuan ). Pour dire «calculer», la langue chinoise moderne utilise encore des termes comme yansuan ou tuisuan , dont le sens premier est, respectivement, «manœuvrer les baguettes», «pousser les baguettes». Peut-être issues des tiges d’achillée à usage divinatoire, ces baguettes en bambou, ivoire ou métal, longues d’une dizaine de centimètres et de section circulaire, triangulaire ou carrée, étaient placées soit sur une quelconque surface horizontale, la table à compter, soit aussi, vraisemblablement, sur un échiquier dont les cases offraient des repères naturels permettant de distinguer les divers ordres d’unités, ou même de «mettre en mémoire» le résultat d’un calcul intermédiaire. Cet ensemble instrumental permettait non seulement d’effectuer les opérations courantes de l’arithmétique élémentaire, mais aussi d’exécuter des algorithmes beaucoup plus complexes: opérations sur les polynômes, résolutions d’équations numériques.

Le boulier, qui est encore très répandu en Extrême-Orient, se compose de deux étages de boules mobiles enfilées sur des tringles serties dans un cadre en bois, et séparées par une barre transversale. Depuis les Ming, il en existe plusieurs variétés qui se différencient soit par le nombre de tringles qui les composent (27 au maximum), soit par le nombre de boules par tringle (5 en bas et 2 en haut, ou bien 5 + 1, ou 4 + 1); les boules du bas valent chacune une unité, et celles du haut cinq unités. L’origine de cet instrument, dont l’utilisation suppose la mémorisation de règles rimées très différentes de celles qu’énoncent nos tables, reste mal connue. On le considère généralement comme un perfectionnement tardif des anciennes baguettes à calculer survenu au plus tôt sous la dynastie des Yuan, voire des Song. Toutefois, certains historiens comme Yamazaki Yoemon le font dériver du boulier romain, car un ouvrage chinois, dont certaines parties pourraient remonter aux Han, le Shushu jiyi (Les Traditions de l’art calculatoire ) contient une description d’un instrument à calculer à boules. Mais le boulier ne s’est vraiment répandu en Chine qu’à partir des Ming. Contrairement aux savantes baguettes, il n’a eu d’application pratiquement qu’en arithmétique commerciale.

D’autres instruments de mathématiques d’origine européenne, comme le compas de proportion de Galilée, les réglettes multiplicatives de Neper, la règle à calcul, ont pris beaucoup d’importance à partir du XVII^e siècle.

Les plus ancien traité de mathématiques chinois connu – le Jiuzhang suanshu , ou les Neuf Chapitres sur l’art mathématique – compilé sous les Han, a exercé une influence considérable. Il se présente comme une collection de deux cent quarante-six problèmes, regroupés principalement par rubriques à visées utilitaires: arpentage des champs, échanges de marchandises, travaux de terrassement, impôt et corvée, mesure des distances sur le terrain, etc. Après l’énoncé de chaque question viennent la réponse, le procédé permettant de l’obtenir et, enfin, à la différence des textes égyptiens ou babyloniens, un ou plusieurs commentaires contenant des justifications rationnelles. Bien des méthodes utilisées – règle de trois directe, inverse ou composée, règle de société, algorithme d’Euclide, calcul des triplets pythagoriciens – sont les mêmes que celles d’autres civilisations de l’Antiquité, encore que certains algorithmes – comme, par exemple, celui qui permet de résoudre tout système numérique de n équations du premier degré par réduction de ce qui correspond à notre matrice du système à la forme triangulaire et par substitutions successives (méthode dite «de Gauss») – ne soient attestés qu’en Chine. Les règles d’addition et de soustraction pour les nombres négatifs qu’on y trouve aussi ne sont pas moins originales, car ceux-ci ne sont pas conçus seulement comme des débits financiers, résultats de soustractions «impossibles», mais comme des objets indépendants. À vrai dire, figurés par de simples baguettes noires ou rouges, ces nombres se trouvaient naturellement abstraits du contexte concret qui les avait suscités et, par conséquent, plus facilement assujettis à des manipulations formelles.

Dès la dynastie des Han, les algébristes chinois savaient résoudre sur la table à compter l’équation du second degré qu’ils considéraient comme représentant une opération généralisée, de même nature que l’extraction de racine carrée, elle-même conçue comme une division particulière. Les spécificités de leur technique instrumentale les amenèrent à effectuer les calculs comme dans la méthode de Ruffini-Horner (début du XIX^e s.), méthode bien attestée en Chine au XIII^e siècle.

Dès le début du VII^e siècle, Wang Xiaotong, qui fut reçu docteur en mathématiques à l’issue d’un concours couronnant sept années d’études, connaît l’équation du troisième degré. Sous la dynastie mongole des Yuan, l’ermite (1192-1279) et le professeur itinérant Zhu Shijie (vers 1300) développent une algèbre de polynômes (tianyuan shu ) mettant en jeu jusqu’à quatre inconnues. Ils y parviennent en affectant les baguettes correspondant aux coefficient numériques des monômes à des places particulières de la table à compter. L’équation finale d’un problème résultait soit d’une soustraction entre deux quantités égales calculées verbalement de deux façons différentes, soit de l’élimination successive des variables entre systèmes polynômiaux. C’est une généralisation de ces méthodes qui conduira le mathématicien japonais Seki Takakazu (1642-1708) à découvrir les déterminants, indépendamment de Leibniz, à la fin du XVII^e siècle. Les procédures chinoises conduisaient à n’envisager que la forme unique f (x ) = 0, contrairement à celles des arabes qui estimèrent longtemps nécessaire de distinguer d’innombrables cas d’équations pour éviter les quantités négatives. En revanche, les mathématiciens chinois ne s’intéressaient pas aux solutions d’équations «par radicaux», mais seulement à l’expression numérique des racines.

Vers les XI^e-XII^e siècles, le triangle dit «de Pascal» apparaît en Chine en tant que moyen de calcul des coefficients du développement de (a + b )ⁿ , mais sans aucun lien avec la combinatoire, domaine pratiquement inconnu des Chinois.

Vers 330 avant J.-C., les Mohistes élaborent un ensemble de définitions mathématiques analogues à celles d’Euclide, mais leur tentative reste sans lendemain, et on chercherait vainement la moindre trace de raisonnement axiomatico-déductif dans la géométrie chinoise, science essentiellement appliquée, qui s’occupe de la planimétrie et de la stéréométrie d’objets comme le champ en forme de corne de bœuf, en forme de van, la digue, le rempart, le mur de douve de fortifications. Il est caractéristique que la plupart des mots conservent leur sens courant, et c’est pourquoi il arrive souvent que plusieurs termes s’appliquent à la même figure abstraite. En outre, l’importance des concepts de perpendiculaire et d’aire, ainsi que l’absence de la notion d’angle sont aussi typiques de cette géométrie que de la géométrie babylonienne. Pourtant, certains auteurs n’ont pas estimé superflu de prouver ce qu’ils affirmaient: Liu Hui (III^e s.) explique des résultats d’algèbre élémentaire et de géométrie (théorème de Pythagore, diamètre du cercle inscrit dans un triangle, identités) en se servant d’un principe d’équidécomposabilité (invariance de l’aire ou du volume d’une figure par fragmentation et réassemblage des divers morceaux); à cet effet, il utilise des pièces colorées qu’il manipule à la manière d’un puzzle. Au XIII^e siècle, Yang Hui utilise le même principe pour trouver la somme de séries. Zu Kengzhi (V^e s.) justifie le calcul du volume de la sphère en appliquant le principe dit «de Cavalieri» à un solide obtenu par intersection de deux cylindres égaux se pénétrant orthogonalement. Liu Hui, déjà cité, approche l’aire du cercle par celles d’une suite de polygones réguliers inscrits de 6 x 2ⁿ côtés (n = 1, 2, ..., 5) et parvient à l’encadrement:

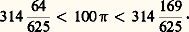Deux siècles plus tard, grâce à un raffinement de ce procédé, Zu Chongzhi en déduit l’excellente approximation 神 = 355/113, dite communément «de Métius» (1586). Mais la géométrie déductive ne commence à être connue en Chine qu’à partir du XVII^e siècle, grâce à une traduction partielle des Éléments d’Euclide par Matteo Ricci et Xu Guangqi (1607), effectuée à partir d’un manuel de Clavius. De nombreux mathématiciens s’intéressent alors à cette science et parviennent à découvrir des résultats nouveaux pour eux (stéréométrie des polyèdres). Mais ils ne conservent rien de la trame discursive du discours géométrique, sans doute en raison de l’étrangeté pour eux d’un cadre qu’ils ne pouvaient pas ne pas associer aux raisonnements de la scolastique, base des enseignements scientifiques comme religieux des missionnaires, la géométrie chinoise n’étant pas fondée sur la «mise à l’épreuve» d’une langue aux phrases constamment contrôlées du point de vue de leur valeur de vérité à partir de principes axiomatiques immuables agissant sur des objets idéaux, mais sur la manipulation et l’observation cas par cas des particularités de figures tangibles.

Deux types de problèmes de théorie des nombres – le problème dit «des cent volailles» et celui des restes – présentent de l’intérêt pour l’histoire comparée des mathématiques, car on les rencontre aussi bien en Chine, en Inde, en Europe que dans le monde islamique. Dans nos notations, ils s’écrivent:

Dans le premier cas, on demande, par exemple, de trouver le nombre de coqs, poules et poussins, sachant qu’un coq coûte cinq pièces de monnaie, une poule trois, trois poussins une pièce et que cent pièces permettent d’acheter cent volailles. Dès le V^e siècle, Zhang Qiujian sait le résoudre correctement. On le retrouve plus tard chez Mahâvirâ Abû Kâmil, Alcuin, Bhâskara II.

Dans le second cas, il s’agit de résoudre des systèmes de congruences simultanées. Ces questions remontent à Sunzi – mathématicien du IV^e ou V^e siècle de notre ère, qui n’a aucun rapport avec le stratège du même nom – dont le célèbre problème s’énonce: «Déterminer un nombre sachant que si on le divise par 3, 5, 7 les restes valent respectivement 2, 3, 2.» D’autres questions similaires apparaissent également chez Aryabhata I (V^e s.), chez Fibonacci (XIII^e s.)... En 1247, Qin Jiushao en présente pour la première fois une procédure résolutoire complète, dite «du grand développement» (dayan ), qui s’applique à des nombres quelconques. En 1801, dans ses Disquisitiones Arithmeticae , Gauss traite le problème pour des modules premiers entre eux, mais il faudra attendre 1859 pour qu’un autre mathématicien, Lebesgue, en fournisse une solution générale. D’après Libbrecht, les règles chinoises et indiennes pour les problèmes de congruences dayan et ku aka n’ont pas de rapport entre elles. Il semble donc que, si ces problèmes n’ont pas été découverts indépendamment, ils ont été transmis d’une culture à l’autre sans indication de solution.

Les formules sommatoires les plus remarquables sont celles qui apparaissent sans preuves dans le Miroir de jade des quatre inconnues (Siyuan yujian ), de Zhu Shijie (1303), et qui s’appliquent à des séries ayant pour terme général le produit d’un terme d’une suite arithmétique par un naturel, un nombre triangulaire ou un carré. Dans la même voie, Li Shanlan (1810-1882) – le Ramanuja chinois – chercha des solutions de l’équation aux différences finies:

qui généralise la formule de récurrence des coefficients binômiaux et obtient des sommations comme:

Au XX^e siècle, des mathématiciens comme Hua Luokeng, Chen Jingrun, Wang Yuan, se sont rendus célèbres par leurs recherches sur les problèmes de Waring, de Goldbach, et les équations diophantiennes.

Astronomie

L’astronomie (tianwen ) constitue un ensemble de spéculations et de pratiques tournées vers l’utilisation des phénomènes célestes à des fins politiques. Les astronomes-astrologues-calendéristes (chouren ) étaient des fonctionnaires affectés au bureau d’Astronomie (significativement, la nomenclature chinoise des étoiles et constellations s’inspire bien plus de la terminologie administrative que de la mythologie). Le Zhouli (le rituel des Zhou) fournit déjà une description idéalisée de cette institution étatique qui, à travers maintes réformes, se maintiendra jusqu’au XX^e siècle. Son personnel ne jouissait pas d’un statut très élevé et, fréquemment, des étrangers y occupaient une position importante: Indiens sous les Tang, musulmans sous les Ming, organisés en un corps particulier à Nankin, parallèlement à l’Office chinois de Pékin, missionnaires européens dominant le bureau de 1644 à 1826, en raison du déclin de l’astronomie chinoise à une époque où l’Europe se trouvait en plein essor scientifique. Ce bureau d’Astronomie comprenait plusieurs services: instruments, observations, calcul, calendrier, divination, enseignement. Le calendrier comprenait des tables pour la prédiction des mouvements apparents du Soleil, de la Lune et des Cinq Planètes, des pronostics astrologiques induits par les correspondances entre régions terrestres et secteurs du Ciel traversés par ces astres (fenye ), les dates des éclipses, les jours fastes appropriés au déroulement des cérémonies, à la mise en chantier des travaux, etc.

Il existe deux sortes de phénomènes célestes: ceux qui sont périodiques et dont le retour peut être prédit, et ceux qui ne se prêtent qu’à l’observation, car se manifestant sans régularité apparente. L’interprétation de ces derniers relève de l’astrologie, tandis que les autres alimentent la science calendérique (lifa ). Mais le calendrier contient aussi des cycles arbitraires, indépendants de l’astronomie. Sous les Yin, les ritualistes avaient constitué un calendrier sexagésimal comptant soixante jours répartis en six décades, chaque jour étant repéré par la donnée d’un couple dont le premier appartient à une série de vocables dénaires (les dix «troncs célestes», tiangan ), et le second à une série duodénaire (les douze «branches terrestres», dizhi ). À partir de 104 avant J.-C., ce système servit aussi à noter les années, et on l’utilise encore de nos jours. Même après la prise en compte du mouvement du Soleil, l’année fut assimilée à une vaste respiration ponctuée de 24 articulations pneumatiques (ershisi jieqi ), elles-mêmes réparties en 12 coupes respiratoires (jieqi ), et 12 pleins respiratoires (zhongqi ), dont faisaient partie solstices et équinoxes. Dans le calendrier luni-solaire du IV^e siècle avant notre ère, appelé la «norme des quarts» (sifen li ), l’année tropique valait 365 jours 1/4 et, détail typique de l’importance du calendrier, c’est la division du cercle en autant de parties qui leur servit de degré; le mois synodique valait 29,53 jours (en pratique on distinguait des mois de 29 et d’autres de 30 jours). Mais la discordance entre une année de 12 mois lunaires, inférieure d’une dizaine de jours à l’année solaire, les avait amenés à introduire 7 mois intercalaires tous les 19 ans, exactement comme dans le système attribué à l’Athénien Méton (vers 432 av. J.-C.). La période de 76 ans (bu ), dite «de Callipe» (vers 370-330 av. J.-C.) leur livra un accord encore meilleur. Jupiter, qui accomplit sa révolution sidérale presque exactement en 12 ans (en fait 11,86 ans, valeur que devait mettre en évidence Liu Xin sous les Han) leur procura un autre cycle calendérique supra-annuel. Finalement, un grand système de cycles aux périodes multiples les unes des autres leur fournit un modèle capable d’engendrer toutes les configurations successives du ciel physique. Et au bout du plus long d’entre eux, soit 31 920 années, lunaisons, éclipses, révolutions planétaires et cycles sexagésimaux étaient censés se reproduire dans le même ordre. Malgré d’innombrables réformes, ou propositions de réformes (six systèmes différents pour la seule dynastie des Han, une cinquantaine des Han aux Qing), les calendriers chinois, qui resteront toujours luni-solaires, ne connaîtront jamais de changements fondamentaux.

Mais les Chinois ne se sont pas contentés de repérer des cycles calendériques, ils ont aussi observé avec le plus grand soin tous les phénomènes célestes: occultations, conjonctions planétaires, taches solaires, comètes, novae, vapeurs, météores et autres «anomalies» célestes, perçues non comme des réalités physiques objectives, mais comme des symptômes annonciateurs de calamités, invitant le monarque à rétablir un équilibre cosmique perturbé par ses agissements déréglés. Il est vrai que certains souverains, comme l’empereur Wu des Jin (265-290) ou encore Yang des Sui (605-617), s’opposaient à l’astrologie et à la divination, mais leurs cas restent exceptionnels, si bien que les chroniques historiques chinoises fourmillent de données précises: localisation du phénomène observé, durée de visibilité, couleur, variations d’éclat, d’où leur intérêt scientifique encore actuel, même si l’interprétation des sources reste souvent délicate (on doit toujours envisager la possibilité de falsifications). Parmi les relevés de comètes (qui remontent aux Yin), figurent ceux de la comète de Halley dont la plus ancienne observation remonterait à 240 avant J.-C., et qui fut repérée vingt-huit fois en deux millénaires. En 832, soit 700 ans avant P. Apianus, les astronomes chinois remarquent que la queue des comètes pointe toujours à partir du noyau dans une direction opposée à celle du Soleil. Les relevés de taches solaires commencent systématiquement à partir de 28 avant J.-C. Mais les recensements les plus étonnants sont ceux d’étoiles variables, comme les novae ou même les supernovae: à l’inverse des chroniques médiévales européennes ou arabes, qui ne contiennent pratiquement aucune information sur le sujet (la seule exception incontestable est celle de la supernovae de 1006, relevée seulement dans les chroniques des monastères de Benevento et de Saint Gallen), les documents chinois sont d’une grande richesse. Vraisemblablement, le dogme aristotélicien de l’incorruptibilité des cieux, qui a dominé la conscience occidentale jusqu’à la Renaissance, rendait difficilement concevable l’existence d’astres présentant des variations brusques de luminosité. Il faut aussi mentionner la surprenante observation, à l’œil nu, des satellites de Jupiter, 2 000 ans avant Galilée, ainsi que l’ampleur des catalogues d’étoiles dont la tradition remonte aux Royaumes combattants: Shi Shen, Gan De et Wu Xian avaient établi les coordonnées équatoriales de 1 464 étoiles réparties en 284 constellations très différentes de celles imaginées en Occident.

L’originalité de l’astronomie chinoise se mesure, selon la formule de Léopold de Saussure, à son caractère horaire, moyen diurne et équatorial, par opposition à l’astronomie grecque qui était angulaire, vraie, annuelle et écliptique (d’après J. Needham, cette dernière différence constituerait un facteur de supériorité de la science chinoise sur la science occidentale, puisqu’il faudra attendre Tycho Brahe (1546-1601) pour que se généralise en Europe une astronomie instrumentale fondée sur le montage équatorial typiquement chinois, mais aussi caractéristique de l’astronomie moderne). En Chine, le repérage des astres se faisait par rapport au pôle de l’équateur et au méridien, et on se servait à cet effet d’étoiles réparties sur le contour du ciel comme des signaux fixes et permettant de définir vingt-huit régions équatoriales d’extensions très inégales, les xiu . Il y a lieu de rapprocher les xiu chinois des nakshatra indiens et des manazil arabes, mais il est difficile d’en établir la filiation. Ils remontent au moins au XIV^e siècle avant notre ère, et semblent être issus de la recherche de points de repère diamétralement opposés pour déterminer les positions invisibles du Soleil par l’observation des pleines lunes.

Parmi les instruments, il faut noter les horloges à encens, les clepsydres ordinaires (analogues à nos sabliers), les clepsydres polyvasculaires réalisant un écoulement régulier de l’eau, les armilles équatoriales de Guo Shouchang (52 av. J.-C.), ainsi que celle de Zhang Heng (vers 124), associée à un mécanisme de révolution diurne contrôlé par une clepsydre, et, surtout, la tour d’observation astronomique de Su Song (1020-1101), aboutissement d’une tradition amorcée trois siècles plus tôt par Yi Xing et Liang Lingzang. Construite à Kaifeng en 1090, elle abritait une sphère armillaire ainsi qu’une horloge pagode avec des jaquemarts apparaissant à intervalles réguliers pour indiquer l’heure. La marche de l’ensemble reposait sur le mouvement d’engrenages et de chaînes de transmission entraînés par la rotation lente d’une roue à godets alimentés en eau, assujettie à un mécanisme d’échappement, le plus ancien attesté (il faut attendre le XIV^e siècle pour que l’Europe en connaisse l’équivalent). Un autre instrument, le simple gnomon (bi ou biao ), permit au moine tantrique Yi Xing (683-727) d’étudier les variations des ombres solsticiales et équinoxiales en différents points d’une ligne méridienne du territoire chinois longue de 2 500 kilomètres, lors d’une expédition scientifique qu’il organisa en 721-725.

Dès l’Antiquité, les Chinois ont défendu au moins trois théories sur la structure de l’Univers ; celles-ci ont toujours coexisté sans qu’aucune ne se constitue en orthodoxie officielle. La plus ancienne, connue sous le nom de «théorie du ciel couvrant» (gaitian ) a évolué en deux versions qu’expose le Classique arithmétique du gnomon des Zhou (Zhoubi suanjing ), qui fut compilé vers 100 avant J.-C. Dans chaque cas, supposant le Ciel et la Terre soit plats, soit incurvés, mais toujours parallèles l’un à l’autre, et admettant aussi que l’ombre du gnomon varie régulièrement, elles aboutissent à un univers de dimensions finies dans lequel le Soleil joue le rôle d’une étoile circumpolaire. Une autre théorie, dite «du ciel enveloppant» (huntian ), dépend de la sphère armillaire (huntian yi ), et repose sur l’idée d’un univers en forme d’œuf dont la Terre serait le jaune. Une troisième théorie, attribuée à Qimeng (vers le II^e siècle), et dite «fruit du travail de la nuit» (xuanye ) soutient que les corps célestes flottent librement dans un univers infini.

Contrairement à une idée répandue, l’astronomie chinoise est aussi une astronomie mathématique. Mais, à la différence de celle des Grecs, ses déductions, fondées sur des formules d’interpolation par des polynômes de degré 2 ou 3, ne reposent ni sur des modèles géométriques cinématiques, ni sur l’idée de lois de la nature immuables, les penseurs chinois estimant foncièrement irrégulière la marche d’un cosmos en perpétuelle évolution.

Techniques

La science, qui a pour objet le savoir, et la technique, tournée vers les applications concrètes, s’appuient fréquemment l’une sur l’autre. Dans le monde chinois, ces deux domaines complémentaires ont toujours été remarquablement solidaires, mais ce pourrait être une erreur d’interpréter ce fait comme une donnée proprement chinoise.

L’Occident et la Chine n’ont pas connu des modes de développement concomitants, et c’est pourquoi certaines techniques sont apparues chez l’un ou l’autre avec de grands décalages dans le temps. Bien plus que d’«avances» ou de «retards», ces décalages témoignent de l’originalité des civilisations, et il est naturel qu’il y ait eu des échanges: l’Occident médiéval n’a pu connaître certaines techniques essentielles que grâce à l’apport chinois.

L’invention du papier, que la tradition attribue à l’eunuque Cai Lun, au début du II^e siècle de notre ère, est en fait le résultat d’un long processus amorcé deux siècles plus tôt. L’analyse physique et chimique de fragments de papier remontant au I^er siècle avant notre ère, découverts lors de fouilles au Lobnor en 1935, puis, plus récemment, au Shenxi en 1957, a permis d’en préciser les étapes. Les papiers les plus anciens sont à base de chanvre, mais peu à peu les matériaux se sont diversifiés: écorce de mûrier, bambou, lin, paille de riz ou de blé. Les techniques de cette fabrication seraient passées en Occident grâce aux contacts entre Chinois et Arabes en Perse et en Transoxiane, avant le milieu du VIII^e siècle. Le papier, support de l’écriture, de la peinture, de l’estampage, sert aussi de monnaie (dès le IX^e siècle). D’abord utilisée pour la reproduction de textes bouddhiques, la xylographie intervient rapidement dans la fabrication des livres (IX^e-X^e s.). Elle devait conserver un rôle prépondérant en dépit de l’invention de l’imprimerie à caractères mobiles (1086), qui connut son plus grand essor en Corée à partir du XV^e siècle.

La plus ancienne mention connue de la poudre à canon se trouve dans un ouvrage d’alchimie chinois qui date du milieu du IX^e siècle (en Europe, c’est Roger Bacon qui y fait allusion le premier en 1267). Contrairement à une opinion répandue, selon laquelle celle-ci n’aurait été utilisée en Chine que dans la fabrication des feux d’artifices, la poudre eut des applications militaires dès le X^e siècle. Des projectiles incendiaires, puis le lance-flammes apparaissent d’abord (avant 950); viennent ensuite roquettes en tubes de bambou, bombes, grenades et flèches incendiaires vers 1000; en 1161, les armées Song l’emportent sur les Jürchen grâce à des catapultes à grenades explosives (pilipao ).

Le fer apparaît en Chine vers le VI^e siècle avant notre ère, longtemps après sa découverte en Asie Mineure, six siècles plus tôt. Mais il est remarquable que, à la différence de l’Occident, le monde chinois ait très vite appris à le fondre, sans faire grand cas de la forge et du martelage. De nombreux objets datant de l’époque des Royaumes combattants – outils, armes, monnaies –, mis à jour à partir de 1950, en témoignent. D’après J. Needham, ce développement exceptionnellement rapide serait dû à la longue expérience acquise par les Chinois en matière de fusion du bronze, à l’utilisation de soufflets avec cylindres et pistons, ainsi qu’aux particularités des matériaux employés: minerais à haute teneur en phosphore permettant une fusion du fer à température moindre, argile réfractaire. La maîtrise de la technologie du fer permit, en particulier, la fabrication de chaînes pour ponts suspendus et d’attaches pour ponts à arches segmentées, comme celui de Zhaoxian, au Hubei (VII^e s.). L’acier (vers 200 av. J.-C.) semble avoir d’abord été produit par cémentation, puis par cofusion, selon un procédé du VI^e siècle, ancêtre de celui de Siemens-Martin.

L’attelage antique du cheval se fondait sur la traction par la gorge de l’animal, ce qui, gênant sa respiration, l’affaiblissait. Dès l’époque des Royaumes combattants, ce dispositif antique est remplacé par un procédé plus rationnel: la bricole de poitrail. Le collier d’attelage apparaît vers les V^eVI^e siècles; l’ensemble permet la traction de plus lourdes charges avec moins d’animaux. La maniable brouette apparaît très tôt. L’Europe ne connaîtra ces techniques qu’au cours du Moyen Âge.

La construction navale ne s’est pas présentée de la même façon en Chine et en Europe: les jonques chinoises, capables de transporter jusqu’à un millier d’hommes, n’ont pas de quille; leur proue, peu différente de leur poupe, n’est pas faite de bordages se rejoignant en étrave. De la forme rectangulaire de leur coque découle naturellement, d’après J. Needham, leur compartimentage par des cloisons étanches, ainsi que l’adoption du gouvernail d’étambot (I^er s. en Chine, XII^e s. en Europe). Suspendu à des câbles, donc facilement relevable, le remarquable gouvernail mobile, qui apparaît sous les Song, ne repose pas sur des charnières fixées à l’étambot, comme dans le cas des navires européens.

La boussole marine, issue de la pratique de la géomancie, apparaît pour la première fois sur les bateaux cantonais à la fin du X^e siècle; la déclinaison magnétique est connue dès le XI^e siècle. Il importe aussi de noter l’originalité de la cartographie quantitative chinoise, fondée sur un réseau de parallèles équidistantes nord-sud et est-ouest (III^e s.).

Bien d’autres innovations apparues bien plus tard en Europe qu’en Chine témoignent de l’originalité de cette dernière à l’époque médiévale. Mais, à partir des XIV^e-XV^e siècles, la Chine, contrairement à l’Europe, ne connaît aucune modification profonde de ses systèmes scientifiques et techniques. D’où ce «paradoxe» provient-il? Pour certains, comme J. Needham, qui pense pouvoir identifier des groupes sociaux clairement responsables, les uns de l’essor scientifique ancien et les autres du «blocage», les causes les plus importantes seraient d’ordre socioéconomique: faiblesse de la classe marchande chinoise rendue responsable de la stagnation mercantile et manufacturière; rôle néfaste de la classe dirigeante confucéenne, qui méprisait les connaissances pratiques et qui était recrutée par concours sur la base d’une éducation de type quiétiste reposant sur la seule étude des classiques; rôle positif des ermites taoïstes centrés sur l’étude des phénomènes de la nature. Mais ces arguments ont été critiqués à juste titre. Moins faible qu’on ne l’a supposée, la classe marchande chinoise n’était pas plus qu’en Europe particulièrement portée vers les innovations techniques. Les confucéens qui se sont occupés de sciences et de techniques sont plus nombreux qu’on ne l’a dit, tandis que les milieux dirigeants ont souvent attaché de l’importance au taoïsme. Mais pour d’autres, les causes essentielles du blocage seraient d’ordre intellectuel: faiblesse de la logique chinoise corrélative du manque de développement de la géométrie euclidienne. Mais, à nouveau, cette explication n’emporte pas l’adhésion: Les pays de l’Islam qui possédaient cette logique ont cependant connu le «blocage». Mais il n’est pas certain qu’il soit pertinent de parler de blocage, car il faudrait d’abord prouver que la Chine devait de toute nécessité s’engager sur la voie de notre modernité et qu’elle aurait échoué à y parvenir.

Encyclopédie Universelle. 2012.